2 (базовый уровень, время – 3 мин)

Тема: Анализ таблиц истинности логических выражений.

Что проверяется:

Умение строить таблицы истинности и логические схемы.

2.7. Алгебра логики. Понятие высказывания. Высказывательные формы (предикаты). Кванторы существования и всеобщности. Логические операции. Таблицы истинности. Логические выражения. Логические тождества. Логические операции и операции над множествами. Законы алгебры логики. Эквивалентные преобра зования логических выражений. Логические уравнения и системы уравнений. Логические функции. Зависимость количества возможных логических функций от количества аргументов. Канонические формы логических выражений.

2.6. Умение строить логическое выражение в дизъюнктивной и конъюнктивной нормальных формах по заданной таблице истинности; исследовать область истинности высказывания, содержащего переменные; решать несложные логические уравнения

Про обозначения

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,¬), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает  Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,¬), что еще раз подчеркивает проблему.

Что нужно знать:

·    условные обозначения логических операций

¬ A,                     не A (отрицание, инверсия)

A Ù B,      A и B (логическое умножение, конъюнкция)

A Ú B,      A или B (логическое сложение, дизъюнкция)

A → B                     импликация (следование)

A º B                     эквивалентность  (равносильность)

·    операцию «импликация» можно выразить  через «ИЛИ» и «НЕ»:

A → B = ¬ A Ú B или в других обозначениях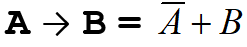

·    иногда для упрощения выражений полезны формулы де Моргана:

¬ (A Ù B) = ¬ A Ú ¬ B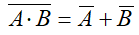        

¬ (A Ú B) = ¬ A Ù ¬ B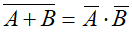        

·    если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем  – «ИЛИ», «импликация», и самая последняя – «эквивалентность»

·    таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных

·    если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);

·    количество разных логических функций, удовлетворяющих неполной таблице истинности, равно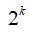 , где 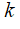 – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 2³=8 строчек, если заданы только 6 из них, то можно найти 2^8-6=2²=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)

·    логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)

·    логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)

·    логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно

·    эквивалентность АºB  равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1