1 (базовый уровень, время – 3 мин)

Тема:  Использование и анализ информационных моделей (таблицы, диаграммы, графики).

Что проверяется:

Умение представлять и считывать данные в разных типах информационных моделей (схемы,

карты, таблицы, графики и формулы).

2.10. Модели и моделирование. Цели моделирования. Адекватность модели моделируемому объекту или процессу. Формализация прикладных задач. Представление результатов моделирования в виде, удобном для восприятия человеком. Графическое представление данных (схемы, таблицы, графики.

2.1. Умение использовать компьютерно-математические модели для анализа объектов и процессов: формулировать цель моделирования, выполнять анализ результатов, полученных в ходе моделирования; оценивать адекватность модели моделируемому объекту или процессу; представлять результаты моделирования в наглядном виде.

Что нужно знать:

·      граф – это набор вершин и соединяющих их ребер; он описывается в виде таблицы (матрицы смежности или весовой матрицы)

·      чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки

·      рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 4 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 4; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет

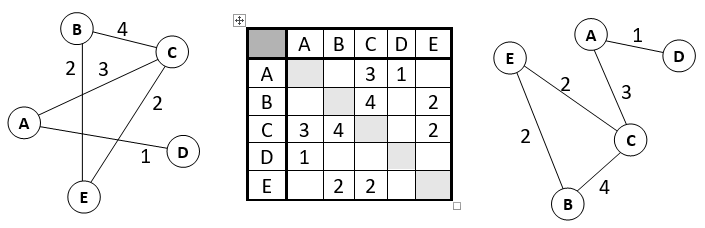
·      обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее

·      в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)

·      во многих задачах вес – это длина дороги из одного пункта в другой; для рассмотренного примера длина дороги из А в С равна 3, дороги из А в Е нет

·      степень вершины – это количество рёбер, которые соединены с этой вершиной; при определении степени вершины по таблице нужно считать число непустых ячеек весовой матрицы в соответствующей строке (или столбце); в примере степень вершины А равна 2 (в первой строке две непустых ячейки со значениями 3 и 1)